Python 计算完全伽马函数,与不完全伽马函数相比,完全伽马函数更难实现,其中有多种近似方法。更多相关信息,请访问http://dlmf.nist.gov/5。Python的math库中有一个可用的版本,它实现了一个广泛适用的近似。
我们对完全伽马函数的完整通用实现并不感兴趣,只关心两种特殊情况:整型值和二分值。对于这两种特殊情形,可以得到精确的解,而不需要依赖近似。
对于整数值,\tau_n=(n-1)!。整数的完全伽马函数可以依赖此前定义的阶乘函数。
对于二分值,有一个特殊形式:
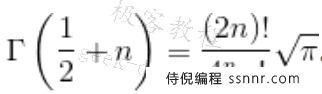
它包含一个无理数 \sqrt{\pi},因此只能使用float或Fraction对象来近似表示。
如果使用合适的Fraction值,那么可以用以下几个简单用例来设计一个函数:一个integer数值、一个分母为1的Fraction值和一个分母为2的Fraction值。可以如下所示使用Fraction值:
sqrt_pi = Fraction(677_622_787, 382_307_718)
from typing import Union
def Gamma_Half(
k: Union[int, Fraction]
) -> Union[int, Fraction]:
if isinstance(k, int):
return fact(k-1)
elif isinstance(k, Fraction):
if k.denominator == 1:
return fact(k-1)
elif k.denominator == 2:
n = k-Fraction(1, 2)
return fact(2*n)/(Fraction(4**n)*fact(n))*sqrt_pi
raise ValueError(f"Can't compute Γ({k})")
将这个函数称为Gamma_Half是为了强调它只适用于所有整数二分数。对于整型值,可使用前面定义的fact()函数。对于分母为1的Fraction对象,可使用同一个fact()定义。
如果分母为2,可以使用更复杂的闭形式值。我们对值 4^nn! 显式使用了一个Fraction()函数,还为无理数 \sqrt{\pi} 提供了一个Fraction近似。
一些测试用例如下所示:

也可以用合适的Fraction值来表示它们。无理数的表示(平方根和π)往往会生成数值很大且可读性很差的分数。可以使用更易读的分数形式,如下所示:
>>> g = Gamma_Half(Fraction(3, 2)) >>> g.limit_denominator(2_000_000) Fraction(291270, 328663)
这里给出的值,限制了其分母小于200万,这样就得到了易读的6位数值,可以用它们来进行单元测试。
版权声明:本页面内容旨在传播知识,为用户自行发布,若有侵权等问题请及时与本网联系,我们将第一时间处理。E-mail:284563525@qq.com




